✔ 본 포스팅은 20/10/10 ~ 20/12/26 동안 진행하는 가짜연구소 딥러닝기초이론스터디를 통해 학습한 내용입니다.
✔ 본 포스팅은 스탠포드 대학의 cs231n 강의를 정리한 내용입니다.
이번 강의에서는 NN을 훈련시키는 나머지 방법들에 대해서 공부한다.
지난 시간에는 가중치초기화, 학습률설정, 배치정규화 등에 대하여 배웠고, 이번 강에서는 NN을 더 최적화시키기 위해
1. Gradient update의 방법들 2. Regularization방법들 을 중점적으로 공부한다.
Optimization 방법
NN의 loss가 최저인 지점을 찾아가기 위해 backpropagation을 거듭하게 되는데 가장 지름길로 빠르게 가기 위한 gradient update에는 여러 방법이 있다. 하나씩 살펴보자!
1. SGD : Stochastic Gradient Descent
2. Momentum
3. Nestero Momentum
4. AdaGrad update
5. RMSProp update
6. Adam
Stochastic Gradient Descent (확률적 경사하강법)
1. 개념

- 초기에 설정한 학습률을 이용하여 손실함수(loss)의 값이 최소가 되는 방향으로 가중치를 업데이트하게 된다.
- $\alpha$ = learning_rate
- dx = x에서의 loss에 대한 기울기
2. SGD의 단점
단점1 : 느리다.


loss 함수가 f(x, y) = $x^2+y^2$ 같은 그래프라면 오른쪽 빗살무늬토기처럼 아래쪽으로 볼록한 공간의 그래프가 나올 것이다. 이 때 x와 y에 대하여 dx, dy 2가지의 도함수가 있을 것이고, 이 두 벡터의 합방향으로 gradient는 개선될 것이다.
이 때 수평방향으로는 기울기 변화가 작고, 수직방향(파란색 긴 화살표)은 빗살무늬토기에서 위아래방향이기 때문에 기울기변화가 가파르다. 이 두벡터의 합방향으로 움직여야 하므로 바로 가파른 방향으로 내려가지 못하고 약간 사선으로 지그재그하면서 가장 아래 최저점에 도달하게 된다.
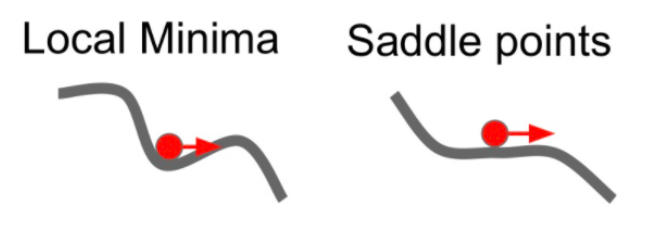
단점2 : local minima와 saddle point

① Local minima의 문제 (위쪽 그래프)
- loss 함수에 기울기가 0인 부분이 있는 경우, 더 이상 가중치 업데이트가 되지 않고 멈춰버리게 된다. (x += learning_rate * dx 에서 dx가 한번 0이 되면, 그 지점을 벗어나지 못하게 된다. 더 내려가면 loss의 진짜 최저점이 있는데, 그 전에 멈춰버린다.)
- 2차원 그래프에서 흔히 겪는 문제
② Saddle point의 문제 (아래쪽 그래프)
- 이 경우는 고차원 그래프에서 흔히 생기는 문제이다.
- 완벽히 기울기가 0은 아니지만, 그 주변이 굉장히 완만해서 가중치업데이트가 느리게 진행하고 그곳에 안주하게 된다.
Monkey Saddle
- 왼쪽같이 생긴 Monkey Saddle이란 그래프가 있다.
- 가운데 넓고 거의 평평한 부분으로 가중치가 업데이트 되면, 그 주변의 기울기도 굉장히 완만하기 때문에 업데이트가 매우 더디게 진행되고 거의 멈춰버리는 현상이 생긴다.
❗ 기울기가 0이 되어도 멈추지 않게 하는 힘이 필요한 것이다!
SGD+Momentum 방법
SGD의 local minima와 saddle문제를 해결하기 위해 "Momentum"이란 방법을 결합하게 된다.
1. 개념

- 가중치 x를 업데이트할때, (가)속도 vx의 개념이 추가되었다.
- 모멘텀은 물리에서 운동량의 개념이다. 공이 언덕을 내려오다가 기울기가 0인 지점을 만났더라도 이때까지 내려오던 속도에 의해 그 골짜기를 지나 계속 굴러갈 수 있을 것이다. 이렇게 이때까지 내려오던 속도의 개념을 추가했다.
t → t+1 지점으로 이동한다고 가정하자.
(1) 1단계 : 속도 업데이트
→ t+1지점에서의 속도를 직전단계인 t지점에서의 속도를 기반으로 예측
한다. $v+{t+1}$은 직전지점에서의 속도 $v_t$와 기울기 dx( $\nabla
f(x_t)$를 고려하여 업데이트하고, 이 때 기울기가 너무 빠르게 변하는 것을 제한하기 위해 마찰계수 $\rho$ (rho)를 적용하게 된다.
이 때 rho는 경험적으로 0.99나 0.9를 사용한다고 한다.
(2) 2단계 : 가중치업데이트
→ loss함수에서 t+1지점은 최종적으로 직전지점 $x_t$에서 학습률 $\alpha$와 t+1지점에서의 예측속도를 고려해 업데이트 된다.
아래 코드식에서는 위의 v가 vx로 표현되었다.
2. SGD와의 차이점


다시 한번 요약하자면,
모멘텀방식은 $x_{t+1} = x_t - \alpha(\rho v_t + \nabla f(x_t))$
SGD방식은 $x_{t+1} = x_t - \alpha (\nabla f(x_t) )$
가중치업데이트에 직전스텝의 속도 $v_t$ 가 고려되었다는 점이 가장 큰 차이다.
이 $v_t$ 역시 이전의 모든스텝의 속도가 누적된 결과일 것이고, 왼쪽 그래프에서 보듯이, 이 속도항 때문에 SGD에서 이동할 거리보다 모멘텀방식은 더 큰 스텝으로 뛰어가게 된다.

Nestero Momentum 방법
다음은 모멘텀방식을 약간 더 업그레이드 한 방법이다.
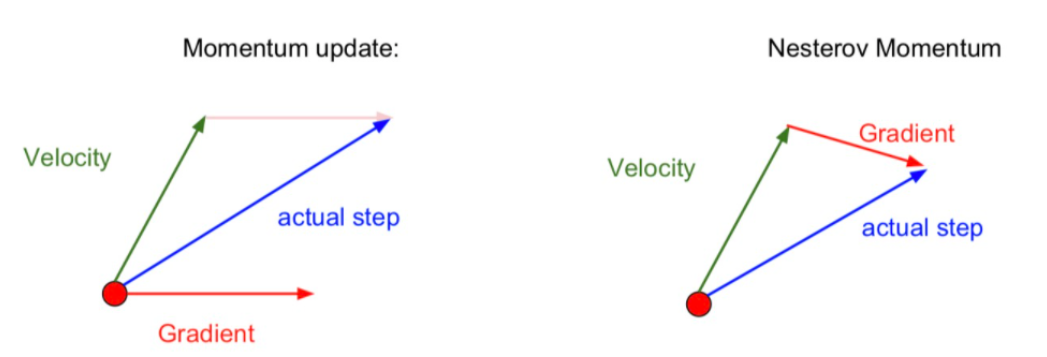
기존의 모멘텀은 직전지점의 gradient와 velocity벡터의 합벡터로 다음 스텝의 지점을 구한다.
Nestero Momentum방식은 직전지점의 velocity벡터의 종착점을 예상해서, 그 지점에서의 gradient벡터를 합하여 다음스텝의 지점을 구하게 된다.
1. 개념


기존의 모멘텀식과 비교해보자.
파란박스 부분이 달라졌다. (학습률 $\alpha$는 v 또는 x 업데이트할 때 곱하게 되는데, 찾아보니 글마다 어디에 곱하는지가 다른걸보니 두 스텝중 한번만 적용해주면 되나 싶다..)
직전지점 $x_t$에서 속도벡터만큼 이동한 지점! 에서의 기울기 $\nabla f()$ 를 이용해 $x_{t+1}$의 업데이트 지점을 구하게 된다.
+코드식
그런데 이 방식은 코드로 나타낼 때, 이미 구성되어 있는 기본적인 optimization algorithm의 API 코드와 조금 구조가 달라서 호환성이 떨어진다고 한다. 그래서 살짝 원래의 기울기업데이트방식과 비슷하게 식을 변환시켜준다.

이 식을 조금더 부연설명하자면, (1)번과 같이 learning_rate $\alpha$ 에 직전스텝의 기울기 dx를 곱하는 식을 쓰기 위해
왼쪽의 f()에 들어가는 항인 $x_t +\rho v_t$ 를 새로운 벡터로 퉁쳐서 $\tilde x_t$ 로 치환해주고 식을 변환한다.

조금더 자세한 계산식이고,
결과적으로 (2)번줄의 다음스텝의 x를 구할 때
$\tilde x_{t+1}$ 를 다음스텝으로 치환하여 계산한
$x_{t+1}= \tilde x_t - \rho v_t + (\rho +1) v_{t+1}$ 으로 코드 표현이 가능하다.
=> 방향을 미리 예측하고 가기 때문에 모멘텀보다 좀 더 빠르다고 한다. (근데 실제로는 잘 안쓴다고도...?)
AdaGrad 방법
1. 개념

- dx의 제곱에 루트를 씌운 값을 x값 업데이트할때 나눠주는 방식이다.
- 여기서 1e -7 값은 0으로 나눠주는 것을 방지하는 아주 작은 값이다.
- grad_squared (cache라고도 함)는 제곱값으로 무조건 양수이고, 계속 이전의 값이 누적되어 증가하게 된다.

<- 이렇게 x값을 업데이트하게 된다.
이런 방식을 per-parameter adaptive learning rate method 라고 하는데, 파라미터 x들 마다 다른 학습률을 제공하게 된다는 뜻이다.
+ 특징

=> 수직축과 수평축의 업데이트 속도를 적절히 맞춰준다.
: 수평축의 dx와 수직축의 dy가 있다고 하면, 수평축은 dx가 작아서 가중치 업데이트시에 나누는 기울기 값이 작아서 업데이트량이 커질테고, 수직축은 가파르니 dy가 커서 나누는 기울기값이 크기 때문에 업데이트량이 줄어드는 효과로 둘의 차이가 어느정도 상쇄된다.
+ 문제점
이 cache값이 계속 누적됨으로 인해 뉴럴네트워크의 학습이 진행되다보면 가중치가 0이 되어 학습이 종료될 수 있다.
RMSProp
AdaGrad의 학습종료 문제를 개선한 알고리즘이다.

- 누적된 grad_squared항에 decay_rate를 곱하고, 현재의 dx항에는 (1-decay_rate)를 곱해 grad_squared가 누적되는 속도를 줄여준다.
- 보통 decay_rate는 0.9나 0.99를 사용한다.
Adam 방법 ⭐

- 일종의 RMSProp + Momentum 을 합친 방식이다.

# Bias 설명추가하기
# Adam 이해하기
다양한 경사하강법알고리즘에서 최적의 Learning_rate는?

- 위의 모든 경사하강법 알고리즘은 학습률을 하이퍼파라미터로 갖는다.
- 최선의 방법은 초기에 큰 학습률을 사용해 빠르게 최소 loss로 수렴하도록 하고, 뒤로 갈수록 학습률을 낮추는 방식이다.
1) step decay : epoch을 돌 때마다 일정한 간격으로 학습률을 감소시킨다.
2) exponential decay , 1/t decay 등이 있는데 현실적으로는 exponential decay를 많이 사용한다.
1차근사과 2차근사
이때까지 우리가 loss함수의 최저점을 찾기 위해 사용한 경사하강법은 1차미분방식이었다.
$$x_{n+1} = x_n - \frac{f(x_n}{f^\prime(x_n)}$$
솔직히 이 때까지 경사하강법에서 이렇게 업데이트하는게 음 왜그러는거지? 알아봐도 대충 이해하고 까먹고 넘어갔는데
여기서 확실히 이해하고 가자!
뉴턴방법을 통한 최적해 찾기

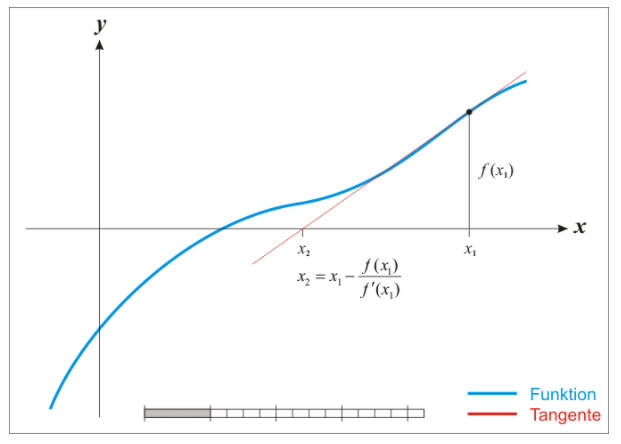
- "미분가능한 함수" y=f(x)에서 y=0인 지점에 도달하기 위해서 $x_{n+1} = x_n - f(x_n)/f^\prime(x_n)$ (n=0, 1, 2, ...)의 수열은 y = 0인 특정 $x_{n}$ 에 수렴하게 된다.
- 위의 영상처럼 진행되어서 결국은 y가 0이 되는 지점으로 간다.
# 참고로, 식은 미분가능한 함수에서 (a, f(a)) 에서의 도함수직선공식을 이용한 식이다.
이에 따라서 $x_{n+1} = x_n - \frac{f(x_n}{f^\prime(x_n)}$ 이렇게 가중치를 업데이트하여 loss가 0(또는 최소)인 지점을 찾아가는 것이다.
2차근사
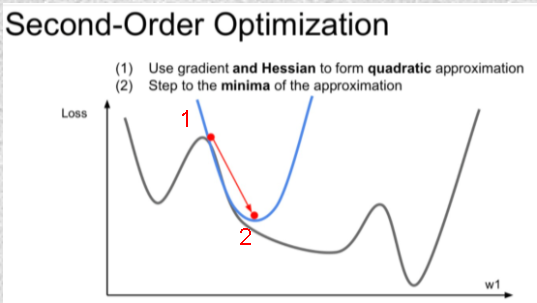

- 강의에서는 loss의 최저점을 찾아갈 때 1차근사 대신 2차근사(Second-Order Optimization)를 하면 더 빨리 최저점에 도달할 수 있다고 했다. 근데 난 2차근사가 뭔지 몰랐다.ㅎㅎ
- 2차 근사는 쉽게 말해서 특정지점에서 기존함수에 근사하는 2차함수를 찾는 것을 말한다. 위에서는 어떤점에서의 기울기를 갖는 1차함수 직선을 구했다면, 여기서는 그 기울기를 갖는 2차함수를 구하는 것이다. 뿐만 아니라 테일러 근사함수 공식으로 n차근사함수까지 얼마든지 구할 수 있다고 함 ^^
- 왼쪽그래프에서 1지점에서의 2차근사함수의 최소값을 갖는 (기울기가 0인 지점이겠죠?) 2번지점이 다음 w로 갱신되고, 그 지점에서 또 2차근사함수를 구하고 같은 스텝을 반복하면 최종 loss가 최소인 지점에 1차근사방식보다 더 발리 도달한다고 한다.

# 제대로 이해하고 설명, 요약다시하기!
Ensembles
- 이 때까지 training data에 대하여 Loss를 최소화시키는 알고리즘훈련방법에 대하여 배웠다.
- 그렇다면 처음보는 validation data에도 이 알고리즘이 잘 작동하게 하려면 어떻게 할까?

이 때 앙상블(Ensembles)이라는 방법을 적용할 수 있다.
- 여러개의 모델을 각각 따로 학습시켜 그 평균값을 이용하는 것이다.
# 추가설명하기
Regularization
(1) Dropout
- train data에 모델이 overfitting되는 것을 줄이고 처음 본 data에도 잘 작동하게 하기 위해서 일종의 regularization으로 dropout이라는 방법을 적용할 수 있다.
1. 개념

- 위와 같은 뉴럴네트워크에서 일부노드를 랜덤하게 0으로 만들어 노드스위치를 꺼버린다.
- 중요한 것은 epoch를 돌때마다 정방향전파과정에서 꺼지는 노드는 계속해서 랜덤하게 변한다는 것이다.
+의미
1. 이 방법은 학습과정에서 redundancy(중복성)을 줄인다라는 의미가 있다.

- 노드를 랜덤하게 끄게 되어도, 남은 노드들이 꺼진 노드가 학습하던 부분을 대신 더 학습하게 된다.
=> 고양이를 볼 때 눈한쪽, 다리 한쪽이 안보여도 고양이라고 짐작할 수 있는 것과 같은 뜻으로 생각했다.
2. 일종의 ensemble 방식이다.
: train epoch를 돌 때마다 랜덤으로 바뀌는 노드의 구성이 변하기 때문에 마치 여러모델의 값을 평균내는 ensemble의 효과를 갖게 된다.
2. test data를 검증할 때의 dropout
- 일반적으로 test data를 평가해볼때는 dropout을 하지 않고, 모든 노드를 켜고 실행한다.
# 아래 설명추가하기



요약
- train 할 때는 네트워크에 무작위성을 줌으로서 train data에 overfitting하지 않도록 한다.
- test 할 때는 이 무작위성을 평균화시켜서 일반화효과를 준다.
=> 앞선 강의에서 배치놈을 적용할 때는 dropout을 사용하지 않아도 된다고 한 이유가 바로 이것이다.
(2) Data Augmentation


- regularization의 일환으로 train data에 변형을 줘볼 수도 있다.
1. 사진 좌우반전
2. 사진을 랜덤하게 자르기
3. 사진 크기 바꾸기
(3) DropConnect
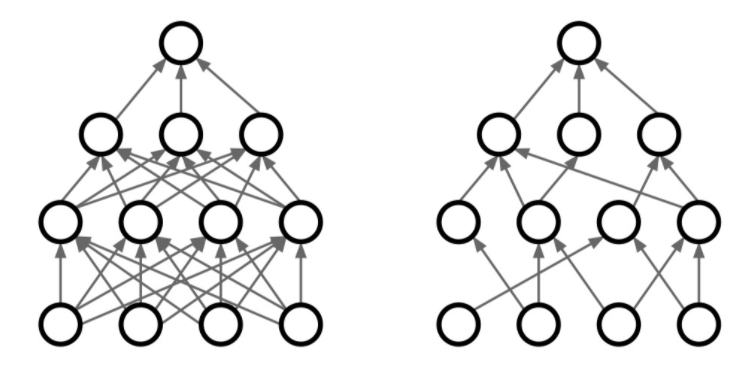
- Dropout은 노드의 activation을 0으로 만드는 것이었고,
- Dropconnect는 노드의 weight matrix를 0행렬로 만드는 것이다.
(4) Max pooling & Stochastic depth


# 요약
regularization에는 batch normalization 이외에도 위와같이 다양한 방식들이 있고, 대개는 Batch norm으로 충분하지만, 일부 overfitting이 과한 경우 dropout을 추가하는 등 적절히 사용하면 된다.
Training transferring
- 학습할 데이터가 충분하지 않을 경우 overfitting이 일어나기가 쉽다.

1. 먼저 많은양의 데이터로 학습시킨 알고리즘을 가져온다! 예를 들어 ImageNet의 사진데이터로 학습시킨 알고리즘은 1000개의 클래스를 분류할 수 있을 것이다.
2. 여기서 C개의 적은 클래스를 분류하는 알고리즘을 만들고 싶다. 이 때 내가 갖고 있는 데이터도 적은 경우
가장 마지막의 Fully Connected layer인 최종 class score를 통해서 사진을 분류하는 layer의 가중치를 초기화한다.
이미지넷에서는 4096*1000 행렬이었는데, 여기서는 4096*4 행렬로 바뀐다.
3. 그리고 이렇게 얻은 마지막 layer만 가지고 우리의 데이터를 학습시킨다.
4. 만약 가진 데이터양이 꽤 된다면? 기존 뉴럴네트워크의 조금더 상위 layer까지 포함하여 학습을 시킬 수 있다.
# 조금 더 자세히 정리하기
출처
www.youtube.com/watch?v=_JB0AO7QxSA&list=PLC1qU-LWwrF64f4QKQT-Vg5Wr4qEE1Zxk&index=7
www.youtube.com/watch?v=5t1E3LZ3FDY&list=PL1Kb3QTCLIVtyOuMgyVgT-OeW0PYXl3j5&index=5
'코딩 독학 > CS231n' 카테고리의 다른 글
| [cs231n] 10강. Recurrent Neural Networks (0) | 2020.12.12 |
|---|---|
| [cs231n] 9 강. CNN architectures (0) | 2020.12.04 |
| [cs231n] 6강. Training Neural Network 1 (0) | 2020.11.14 |
| [cs231n] 5강. Convolutional neural networks (0) | 2020.11.08 |
| [cs231n] 4강. Backpropagation and Neural network (0) | 2020.10.31 |





댓글