✔ 본 포스팅은 20/10/10 ~ 20/12/26 동안 진행하는 가짜연구소 딥러닝기초이론스터디를 통해 학습한 내용입니다.
✔ 본 포스팅은 스탠포드 대학의 cs231n 강의를 정리한 내용입니다.
지난 강의 복습
4강에서는 Backpropagation과 Neural network에 대해서 배운다.
지난 강의를 복습해보자면,

1. input data를 넣어 예측할 각 클래스의 score를 f(x; W) = Wx 라는 함수 (가중합이라고도 함)로 구한다.
2. 이 값을 SVM loss를 구하는식에 넣어 hinge loss를 구한다.
3. train data에 overfitting되는 것을 방지하기 위해 regularization 함수를 더해 최종 Loss를 구한다.
4. 이 Loss가 최소가 되는 parameter W를 구한다.
여기서 4번과정을 Optimization이라고 한다.
최종 Loss함수는 최저점이 하나(?)가 되도록 아래가 볼록하게 설계될 것이고, W를 수정함에 따라 Loss의 크기가 변화할것이다. W를 조금씩 움직이며 W에서의 Loss함수의 기울기가 줄어드는 방향으로 움직이다보면, 기울기가 0 즉, Loss가 최소인 지점의 W를 구할 수 있다는 것이 핵심이다.
Optimization의 속도를 빠르게 하기위해서는 아래로 볼록한 Loss함수에서 최저점으로 이동해 내려갈 때,
가장 경사가 가파른 방향 을 따라 내려가야 할 것이다.
이 때 경사하강법 (Gradient descent)를 사용한다.

경사하강법에는 2가지 방법이 있는데,
직접 lim 를 이용해 함수의 기울기값을 구하는 Numerical gradient 방법과,
증명된 수학공식을 이용해 뚝딱 기울기값을 구하는 Analytic gradient가 있다.
analytic gradient가 더 빠르고 좋다~ (이정도만 생각..)
--
그래서 score계산부터 경사하강법까지 이 과정 전체를 단계별로 나누어 도식화한 것을 계산그래프(Computation graph)라고 한다.

굳이 이렇게 모든 변수와 함수들을 각 노드에 나누어 Computation graph를 만드는 이유는
우리가 곧 배울 Convolutional network의 경우는 위의 예제와 같이 단순하지 않고 엄청 복잡하고 많은 input, weight, 함수들이 있기 때문이다. 수백개의 합성함수는 쉽게 미분할 수 없기 때문에 단계적으로 계산해야 한다.
여기까지가 지난시간의 복습이다.
Backpropagation 역전파
오늘 다룰 내용은 Backpropagation (역방향전파)이다.
위에서 Optimization을 하기 위해서는 Loss함수에 대한 초기 input 데이터인 W의 미분값을 구해야 했다.
하지만 복잡한 모델에서 당연히 모든 W값을 하나씩 대입하고 미분하기에는 시간이 너무 오래걸리고 비효율적이다.
따라서 사용하는 것이 Backpropagation이다.
지금부터 그 내용을 알아보자 🙌

이 한장의 슬라이드로 개념을 잡고 가자. Follow me~
- (x, y, z) 를 input으로 넣어 (x+y)z를 반환하는 함수 f가 있다.
- 이를 Computation graph로 나타내면 그림(2) 와 같다. x와 y를 (+)노드에 넣어 (x+y) 값을 반환하고 이를 q에 저장한다. 그리고 최종적으로 q와 z를 더해 f를 구한다.
- 따라서 q = x+y , f = qz 로 나타낼 수 있다.
⇒ 여기서 f값은 우리가 구하고자 하는 Loss를 의미하고, f가 최소가 되는 parameter (x, y, z)를 구하는게 목표이다.
⇒ Want : 이를 위해 최종 f에 대하여 input (x, y, z)가 미치는 영향을 측정하기 위해 f에 대한 (x, y, z)의 편미분값을 구할 것이다. 저 6처럼 생긴 기호는 델타? 라고 하는데 고등학교때 편미분 할때 dy/dx 한것이랑 비슷한거라고 생각하면 된다.
∂f/∂z, ∂f/∂y, ∂f/∂x를 구하는게 목표인데, 예시의 식은 간단해서 바로 구할 수도 있겠지만, 나중에 여러겹의 합성함수 형태가 됐을 땐 불가능하다. 따라서 Chain rule이란 것을 이용해 최종값부터 바로 전단계의 변수에 대한 편미분값을 단계적으로 구해나가면서 가장 초기변수와 가장 최종변수간의 편미분값을 계산할 것이다.

이 그림을 다시보자. 오른쪽에서 왼쪽으로 편미분을 해나가기 때문에 역방향전파라고 하는 것이다.
f에 대한 q의 편미분값인 ∂f/∂q, f에 대한 q의 편미분값인 ∂f/∂z
그리고 q에 대한 x와 y의 편미분값인 ∂q/∂x, ∂q/∂y가 있다.
∂f/∂z, ∂f/∂y, ∂f/∂x를 구하기 위해 chain rule을 적용해보면 다음과 같다.

각 단계마다 구한 편미분값들을 서로 연쇄적으로 곱해 최종값에서 몇단계 떨어져있는 초기값 사이의 편미분값을 구하는 것이다.
이러한 단계의 가장 기본을 살펴보자.

하나의 노드는 f라는 함수에 의해 계산되고, x와 y라는 input을 받아 z라는 결괏값을 도출해 z 를 마지막으로 Loss를 도출한다고 해보자.
아까와 같이 거꾸로, 최종 Loss에 대한 z의 편미분값을 먼저 구하고, f노드의 결괏값인 z에 대한 x와 y의 편미분값을 각각 구해서, chain rule을 이용해 ∂L/∂z와 곱해주면 최종 L에 대한 x와 y의 편미분 값을 구할 수 있다는 것이 핵심 개념이다.
그렇다면 우리는 backpropagation을 하기 위해서 모든 노드마다 편미분값을 구해주어야 할까? 생각보다 귀찮은데?
아래의 조금더 복잡한 Computation graph를 보자.

여기서는 초기 input이 w0, w1, w2 와 x1, x2 로 2개의 피처 x 에 3개의 weight를 input으로 넣는다.
이를 이용해 Score를 구하는 과정이 빨간박스이다.
Score를 sigmoid 함수의 x로 다시 넣어서 결괏값을 0과 1사이의 수로 만들어 참/거짓을 판단하는 Loss를 구할 것이다.
여기서도 각 노드를 사이에 둔 두 변수 사이의 편미분 값을 구해 빨간숫자로 아래에 나타냈다. 오른쪽에서 왼쪽방향으로 곱하고 곱하고 곱해주면서 backpropagation해주면 당연히 Loss에 대한 input parameter들의 편미분값을 구할 수 있겠지만, 파란색 박스인 sigmoid gate를 주목해보자.
sigmoid함수의 기본형은 알려진 미분공식에 의해서 한방에 미분이 가능하다. 파란부분은 Score에 -1을 곱해 -Score를 만들고 거기에 다시 exponetial을 취해 e의 제곱승에 올리고, 거기에 +1을 해서 분모로 취해 최종 sigmoid함수 값을 구하는 건데, 이 부분은 굳이 노드마다 편미분값을 곱할 필요없이, 한번에 ∂σ/∂x를 계산 가능하단 것이다~
이 외에도 노드 (혹은 gate)마다 쉽게 편미분 gradient를 부여할 수 있는 방법이 있다.

위의 add, max, mul gate란 것인데, 각 노드에 들어온 변수를 덧셈/최댓값반환/곱셈 을 해주는 gate들인 경우 쉽게 편미분값 반환이 가능하다.
(3)번 노드를 보면 a + b를 받아 c에 반환하는 노드이고, ∂d/∂a 를 구하고자 할 때, 그 전단계까지 backpropagation을 진행하여 구해놓은 gradient값인 ∂d/∂c 에 ∂c/∂a 를 곱해주면 구할 수 있는데,
계수가 1인 일차함수 형식의 덧셈공식에서는 미분하면 1이 되므로, 직전노드의 gradient값인 ∂d/∂c를 그대로 보내면된다. gradient를 그대로 보낸다고 해서 gradient distributer라고 하며, 이것은 add gate에서 항상 적용된다.
마찬가지로 mul node에서는 (1)번 노드를 보면, x에 대한 gradient를 구한다 할때 현재노드 gradient에 x*y를 x에 대해 미분한 값을 곱하면 되는데, 역시 편미분하면 x는 사라지고 나머지 y가 상수처럼 남아 해당 값을 곱해주면 된다.
두 변수의 곱에서 편미분하고자 하는 변수말고 상대변수를 곱해준다고 해서 gradient switcher라고 부른다.축
Jacobian matrix 와 input벡터

위에서 본 사진을 다시 끌어옵시다.
사실 이 때까지 x, y, z를 하나의 변수로 보고 개념을 이해했지만, 조금더 심층적으로 들어가봅시다.
실제 데이터세상에서 x와 y 그리고 z는 하나의 '숫자, scalar'가 아니라, 그 안에 다시 여러 성분이 들어있는 d차원의 벡터일 것입니다.
위에서 ∂L/∂x 는 벡터, ∂z/∂x는 matrix가 될 것입니다.
위에서 x벡터가 f gate를 거쳐 z라는 벡터가 출력될 때, z
여기서 자코비안 행렬에 대한 개념이 나옵니다.
자코비안 행렬
angeloyeo.github.io/2020/07/24/Jacobian.html
⬆위 글에서 자코비안 행렬 개념을 이해하고 오시고~
아래의 그림을 보면, f(x) 함수에 대한 input은 4096차원의 벡터이고, 그에 대한 output도 4096차원의 벡터로 나옵니다.
f(x) = max(0, x) 라는 relu함수이고, x<0일때는 y=0, x>0일때는 y=x 일차함수의 형태를 띠죠.
중요한건 에 4096개의 벡터가 하나의 특성변수 안에 있다는거죠!
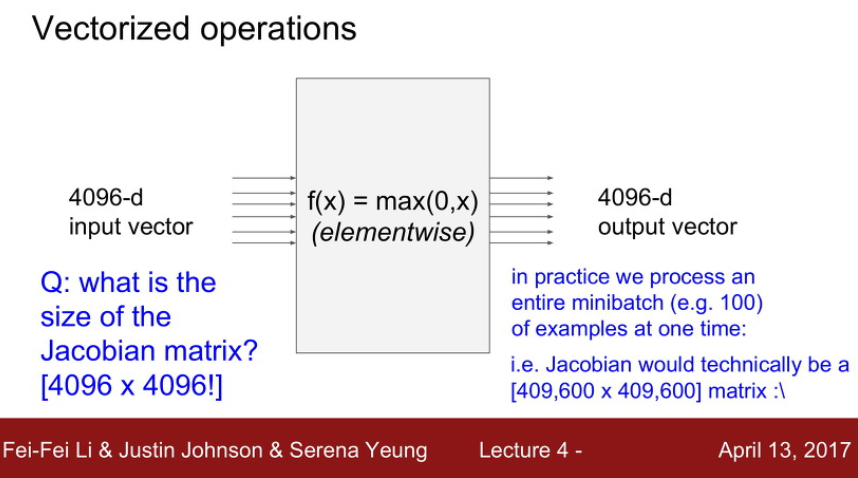
여기서 질문을 던져봅니다.
Q. 4096차원의 input vector가 f(x) gate를 통과하여 4096차원의 output vector가 되었을때 자코비안행렬의 크기는?
A. 4096 x 4096
솔직히 아직 이 부분은 이해가 안 된다 ㅠ
💦 mini batch란?
# (mini) batch size : sample 데이터 중 한번에 네트워크에 넘겨주는 데이터의 수
⇒ 한번의 iteration 에 사용하는 데이터 사이즈를 나누는 이유는 적당히 빠르고 정확하게 gradient descent 를 진행하기 위함입니다. 하나씩 하면 iteration 한번의 시간이 짧지만 데이터 전체 경향을 반영하기 어렵고, 한번에 데이터를 다 주면 iteration 소요시간이 매우 길어지고, 하드웨어에 로딩도 커지기 때문에 적당히 무작위로 100개 정도씩 뽑아서 수행하게 된다.
출처
'코딩 독학 > CS231n' 카테고리의 다른 글
| [cs231n] 6강. Training Neural Network 1 (0) | 2020.11.14 |
|---|---|
| [cs231n] 5강. Convolutional neural networks (0) | 2020.11.08 |
| [cs231n] 과제1. KNN classifiers (0) | 2020.10.29 |
| [cs231n] 3강. Loss function, optimization (0) | 2020.10.23 |
| [CS231n] 2강. L1 & L2 distance (0) | 2020.10.18 |




댓글