✔ 본 포스팅은 20/10/10 ~ 20/12/26 동안 진행하는 가짜연구소 딥러닝기초이론스터디를 통해 학습한 내용입니다.
✔ 본 포스팅은 스탠포드 대학의 cs231n 강의를 정리한 내용입니다.
✔ 아직 이해가 잘 안 되는 부분이 많아서 계속 수정하겠습니다. 😅
지난시간

data-driven approach 로 KNN classifier에 대해 보았고, CIFAR-10 데이터셋으로 실습을 진행하였다. (아직도 다 못함 ㅠㅠ) KNN classifier는 test와 train 이미지간 픽셀값차이를 통해 L2 distance를 구해 거리가 최소인 k개의 train
그리고 train/test data로 나눈 뒤, 최적 hyperparameter를 구하기 위해 검증할때 train data를 K개의 fold로 나누어 돌아가면서 validation set역할을 하여 hyperparameter 튜닝을 하였다.
아래 그림은 KNN classifier를 통해 데이터의 클래스를 구분하는 것이고, 알고리즘의 성능이 최적인 K값 또한 hyperparameter로 검증을 통해 정해야 했다.
하지만, 이경우 모든 traini data와 distance를 구해 시간이 오래걸리고, 사진구분이 정확하지 않았다.

그에 비해 Linear classifier 는 사진의 픽셀을 벡터로 펴고 각 클래스를 구분하는 선형방정식의 가중치 w와 편향 b를 통해 사진을 구분하는 방식으로 더 정확하였다. 단순한 Linear classifier는 w값이 랜덤으로 지정됐고, 이를 더 정확하게 고쳐나가야 했다.
📂 wewinserv.tistory.com/74 ⇒ 설명 매우 굿

예제를 단순화시켜보았다.
고양이, 자동차, 개구리 3개의 class 가 있는 데이터셋에서 f(x,W) = Wx 라는 함수를 이용해 스코어를 구해보았다.
linear classifier인 f(x,W)로 각 이미지의 클래스 예측점수를 보면, 가장 높은 점수인 클래스가 실제정답인 경우는 자동차뿐이다. 실제 클래스 yi 와 선형함수 f(x,W)를 통해 예측한 클래스 간의 차이를 특정 오차함수에 넣어 계산한 값을 L (loss)라 하고 이것을 최소로 하는 w를 구하기 위해 값을 수정하는 것은 경사하강법이라고 하는데, 이번 강의에서는 이 "loss function"을 무엇으로 정할지에 대해 알아보겠다.
multiclass SVM loss (Support Vector Machine)

xi = 이미지, yi = 레이블
sj = 잘못된 레이블의 스코어, syi = 제대로된 레이블의 스코어, 1=safety margin
Li 의 공식을 살펴보자. 0과 sj-syi+1 값 중에 더 큰 것을 Li 값으로 주는 함수이다.
위에서 +1이 safety margin이라고 했는데, 이게 무슨말이햐면 max(0, sj - (syi -1)) 로 식을 살짝 바꿔생각해보면 된다.
⇒ 잘못된레이블의 스코어 > (제대로된레이블의 스코어-1) 라면, loss 는 0이 아닌, 뒤의 값이 선택되므로 0보다 클 것이다.
즉, 잘못된레이블의 스코어에 +1을 해도 정답레이블의 스코어보다 작을때 loss = 0이라고 할 수 있다.
그래서 숫자 +1을 safety margin이라고 한다.
예를 들어보자.

고양이의 training loss는 맞는 레이블에 대한 score는 3.2 (=syi) 이고, 다른 레이블에 대한 loss값을 SVM 공식으로 구하면 sj가 각각 자동차=5.1, 개구리=-7.1 이므로 위와같이 최종 Loss 값은 2.9가 나온다.
>> 정답은 고양인데, 정답인 cat 분류점수는 3.2고, 오답인 car 분류점수에 +1을 하면 (안 해도 이미 크긴 하지만) cat보다 점수가 크니 loss가 있다. 하지만 frog 분류점수는 -1.7로 +1을 해도 cat(3.2)보다 작으니 loss = 0이라 할 수 있다.


이런식으로 고양이, 자동차, 개구리의 현재 w값들로 훈련된 linear classifier에서의 평균 Loss값은 (2.9 + 0 + 12.9) /3이다.
💫 Q. SVM에서 j 와 y_i가 같은경우는 제외하고 있는데, 이유는?
⇒ max(0, syi-syi+1)이 되어 최종 loss값의 평균이 1만큼 증가할 것임
💫 Q. squared hinge loss 를 사용하면?

이 때는 선형함수에서 벗어나므로 차이가 생김
💫 Q. 대개 W 초기화할때는 거의 0에 가까운 작은수로 초기화하는데, 이 때 loss는 ?
⇒ W가 거의 0에 가까우면 sj나 syi나 거의 0이고, Li 값은 max(0, 0+1) =1 들을 (샘플수-1)번 더한 값이 나올 것
⇒ 최초에 학습을 시작할 때, loss값이 어떻게 나올지 예측가능하므로 학습이 제대로 시작됐는지 sanity check가 가능하다.
numpy code

x 는 image의 1차원 벡터, y는 레이블을 나타내는 integer값, W는 파라미터인 weight matrix가 될 것이다.
W와 x 간의 행렬곱을 .dot연산을 통해 구하고, margins[y] 는 j=yi 인경우로 제대로된클래스(yi)를 맞췄을 때는 오차가 0이므로 margins[y] = 0으로 대입한다.

따라서 SVM loss function 을 정리하면 이런데, 약간의 허점이 있다.
N개의 데이터를 f(x,W)에 넣어 구한 스코어와 실제 레이블과의 Loss 가 0이 되는 W를 찾았다면 , 그것은 과연 원앤온리일까? 아니다.
실제로 굉장히 많은 조합의 W는 L=0을 만들 수 있다.
Weight Regularization
원앤온리 W를 구하기 위해 Weight regularization , 표준화라는 과정을 거친다.

W가 얼마나 괜찮은가~ 를 측정하는 것이다.
기존의 Loss function 에 λR(W) 가 추가되었다. 왼쪽 기존의 항은 "학습데이터셋에 최적화되는 W를 찾기" 이고, λR(W) 항은 "테스트데이터셋에 최적화되는 W를 찾기" 이기 때문에 classifier를 학습할때 과적합되지 않고 훈련데이터셋에서의 성능이 조금 떨어져도 처음본 사진으로 테스트를 했을 때 성능이 좋아지도록 일반화한 것이다.
요기서 L1, L2 표준화 등을 사용하게 되는데
bookandmed.tistory.com/27 ⇒ 이전 포스팅에 자세히 설명해놓았다.

예를 들어 x라는 벡터를 classifier w1과 w2를 이용해 f(x,W) = Wx 를 적용하여 score값을 구해보면, w벡터는 transposition하여 행렬곱을 하면 둘다 1이 나오게 된다. 하지만 직관적으로 봤을때, x 벡터의 4가지 feature들에 w1은 첫번째 feature에 몰빵한 가중치를 가지고, w2는 상대적으로 4개의 feature을 모두 염두하게 되는 차이가 있다.
w2는 L2 regularization을 의미하는데, 가능한 모든 feature를 고려하여 가중치를 부여한다는 의미에서 강의에서는 diffuse over everything 이라고 표현하고 있다.
따라서 동일한 score의 W 라면 최대한 가중치가 다양한 feature에 분산돼있는 표준화모델을 선호한다.
Softmax Classifier (Multinomial Logistic Regression)
두번째로 Softmax 라는 Loss function을 소개한다.
일반적으로 로지스틱회귀에서 시그모이드함수는 입력데이터에 대해 0~1 사이의 값을 출력해 0.5를 기준으로 대소비교를 하여 0과 1 어느하나로 분류하는 이진분류에 사용했다. 하지만 분류할 클래스가 3개이상인 경우는 다중분류라고 하고 이때 사용하는 분류기 중 하나가 Softmax Classifier 이다.
강의설명에 앞서 이해가 잘 안 돼서 기본개념을 먼저 정리하고 간다.
출처 : wikidocs.net/35476
소프트맥스 분류기란?
입력데이터 x = [x1, x2, x3, x4] 로 꽃의 종류를 분류하는데 필요한 꽃잎길이, 넓이 등 4가지 특성 원소가 들어있다.
소프트맥스 분류기는 k개의 다중분류를 시행하기 때문에, 가중합을 이용한 첫번째 은닉층의 노드를 k개 만들게 된다.
여기서는 꽃의 종류가 3개라고 생각하고, 출력노드를 3개로 설정하였다.
1. 첫번째 단계에서는 가중합을 이용해 각 레이블에 대한 score를 계산한다. 위의 그림에서는 z값으로 표현했다.
2. z값을 입력데이터로 삼아 Softmax Classifier에 넣고 계산하여 최종 예측값을 구하는데, 잘 보면 3개의 예측값이
0.26 + 0.70 + 0.04 = 1 로 총합이 항상 1로, 각 분류가 정답레이블일 확률을 나타내게 된다.
3. 실제 정답이 두번째 꽃이라면 해당 데이터레이블의 원핫벡터는 [0, 1, 0]일테고, 소프트맥스함수의 예측값은 [0.26, 0.70, 0.04] 이므로 두번째 꽃이 정답일 확률이 가장 높긴 하지만, 여전히 오차가 존재한다. 이 오차를 계산하는 비용함수로 크로스엔트로피함수 를 사용하는데, 뒤에서 다시 설명한다.
소프트맥스 분류기의 함수

이 "Softmax Classifier" 는 어떻게 생긴 함수인지 살펴보자.
우선 첫번째 단계에서 score를 구할 때는 기존에 사용했던 linear classifier 인 s = f(xi, W) 를 사용한다.

그리고 이 부분이 "소프트맥스 함수"이다.
3개의 score가 나왔다면, 3개의 score를 e의 제곱승한 값을 모두더한 분모로 자신의 e의 score제곱승을 나눠준다.

이 함수를 다시 이해하고 가보자.
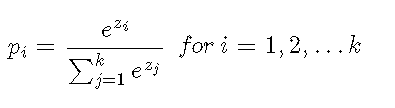
소프트맥스함수가 받는 데이터 input은 분류해야할 레이블의 개수와 같이 k개라고 위에서 언급하였다.
input 벡터를 k개의 원소를 가진 z 라고 하면, i번째 원소는 zi이다. 그리고 pi는 i번째 클래스가 정답일 확률일 때, 소프트맥스 함수는 위와 같이 정의한다.
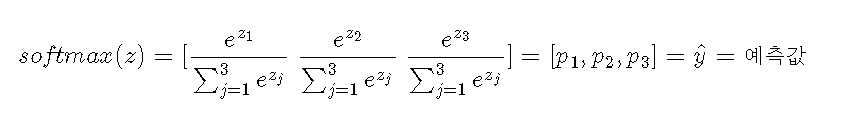
따라서 3개의 클래스가 있는 데이터에서 소프트맥스함수를 돌리면 위와같이 되고, 각각의 p1, p2, p3는 1번째, 2번째, 3번째 클래스가 정답일 "확률"를 나타나게 된다. 소프트맥스함수를 통과하면서 결괏값을 모두 더했을 때 1이 나오는 확률값으로 변환되는 것이다.
다시 강의로 돌아가보면,

이 식은 i번째 input데이터인 xi에서, 정답레이블이 k번째 레이블로 분류될 확률을 나타내고 있다.

실제 xi 데이터의 정답레이블은 yi일때, xi 데이터의 예측값이 yi로 제대로 나올 확률을 로그취한것을 "최대화", 그것에 마이너스를 붙인 위의 식을 "최소화"하는 것이 목표다. (로그를 취하는 것을 수학적으로 여러면에서 좋기 때문)
교차엔트로피

이것이 교차엔트로피 공식이고, 소프트맥스 함수의 예측값의 오차를 구하는데 사용한다.

정리해보면,
1. f(xi, W)로 score 구하기 : 선형분류
2. score들을 exponential (e의 제곱근 형태) 함수의 일종인 소프트맥스함수에 넣어서 각 클래스가 정답일 확률 구하기 (빨강+초록색 박스)
3. 교차엔트로피 Li 를 이용해 Loss 구하기
💫 loss Li의 최소/최대는?

Li함수인 y = - log(x) 그래프에서 보면,
x는 확률이기 때문에 0~1 사잇값이라서 y 는 최소 = 0, 최대 = ∞ 의 값을 갖는다.
💫 W의 초깃값을 거의 0으로 초기화하면 이 때의 loss는 얼마인가?

W가 전부 0이면, 요기서 가장 처음의 score들이 0이 되고, 이를 e의 제곱승으로 올리면 빨간박스값들은 1이되고, 총합이 1인 확률값으로 바꾸면 최종 1/3, 1/3, 1/3 이 될 것이다. 이에 따라 정답레이블에 대한 예측값의 loss는 -log(1/3) 이다.
이를 일반화하면 W가 0일때 loss값은 -log(1/클래스개수) 가 될 것이고, 이 역시 초반에 학습이 제대로 시작되는지 sanity check 용도로 사용할 수 잇다.
SVM 과 Softmax 의 비교요약

위에서 해당 데이터셋 xi의 정답레이블은 3번째 클래스일 때의 각각 SVM과 softmax classifier를 이용해 loss값을 구한 것이다. Softmax의 loss값이 더 적음을 알 수 있고, 실제로도 Softmax가 더 많이 사용된다.
💫 Q. 데이터의 초기 score를 약간씩 바꿨을 때, Softmax와 SVM을 이용한 loss값에 차이가 생기나요?

QQ. 이 말이 맞는지 오늘 스터디에서 질문!
초기의 f(xi, W)를 이용해 score를 구할 때, W를 바꿔서 score를 바꾸면
SVM 은 safety margin인 +1 이 있기 때문에, 쉽게 sj 와 (syi-1) 사이의 역전이 생기지 않아서 loss값은 상대적으로 변화가 없지만, Softmax는 score가 그대로 확률값에 적용되므로 loss에도 변화가 생긴다.
SVM이 robustness(변하지 않은 굳건함?)가 더 크다, 즉 값변화에 둔감하다고 할 수 있다.
Softmax는 모든데이터에 더 민감하다고 할 수 있다.
Optimization
Optimization은 "loss 를 최소화시키는 과정" 이라고 할 수 있다.

다시 위의 내용을 복습하면,
1. W와 데이터 xi를 f(xi, W) 함수에 넣어 score를 구한다.
2. softmax 또는 SVM classifier로 각 클래스에 대응하는 score 들에 대한 loss를 구한다.
3. Loss가 최소화되는 W를 찾고, 여러가지 가능한 W들 중에서 최적 W를 찾도록 Weight regularization을 한다.
4. 최종적으로 Loss 가 최소화되도록 Optimization을 한다.
최적화 전략
따라서 마지막으로 이 "최적화"란 무엇인지 살펴보자.
#전략1. Random search

코드를 돌릴 때 W를 random으로 뽑아내서 여러번 테스트하는 방법이다. 당연히 아무이유없이 해보고, 이 W가 최고네~ 하면 최종 accuracy가 좋을리가 없다.
이보다 더 좋은 방법은 바로 다음 전략이다.
#전략2. Slope 따라가기

loss 함수를 최솟값이 있는 오목한 함수라고 생각했을 때, A와 B 지점에서 미분하여 구한 기울기가 더 작은 점이 우리가 찾는 최소 loss를 갖는 최종 W와 더 가까운 점이라고 생각하고, 이렇게 W를 찾아나가는 것이다.
이것을 Gradient Descent라고 한다.
Gradient Descent
아래의 예시를 보자.

처음 W와 loss값이 저렇다고 하고, 첫번째 차원에 대한 W를 h=0.0001만큼 조금 움직였더니 loss가 살짝 줄었다.
요기서 미분식을 이용해 dW를 구하면 -2.5가 나온다.

두번째 차원의 W를 h=0.0001 만큼 이동하니까 오히려 gradient (dW)가 커졌다.
이런식의 계산법을 numerical gradient 라고 한다.
이런식으로 계산하려면 단점이
1. 정확한 값보다는 근사치를 활용한 계산이다.
2. 시간이 정말 오래 걸린다.
하지만 3. 코드를 작성하기는 쉽다 라는 장점이 있다.

위에처럼 하나씩 숫자로 계산하지 않고, 미분공식을 이용하는 analytic gradient 가 있다.
실제로는 코드작성이 조금 더 어렵지만, 쉽고 빠른 analytic gradient 를 주로 사용한다.
>>실제코드

여기서 step_size = learning rate, α로 일종의 hyperparameter이다.
또 앞에서의 weight regularization에 사용한 λ(람다) 와 같은 hyperparameter를 구하기 위해
validation set으로 교차검증하여 최적값을 찾아주는 것이 우리가 할 일이다.
Mini-batch Gradient Descent
train set의 일부를 이용해 보다 효율적으로 학습하여 gradient를 개선하여 parameter (W 등)를 업데이트하고
mini-batch 를 여러 set로 반복하게 된다. 대개 32, 64, 128, 256 등의 size로 진행한다고 한다.


mini-batch를 사용하면 loss가 위의 그림처럼 왔다갔다하긴 하지만, 결과적으로는 서서히 감소한다.
CNN 이전의 이미지분류방식
전통적인 방법에서는 원래 이미지에서 추출한 feature를 1차원벡터로 쭉 펴서 여기에 linear classifier를 적용했다.

특징 추출하는 방법은
1. Color histogram : Color가 feature가 되어 모든픽셀의 color를 뽑아내고, 이미지 내에 특정색에 해당하는 pixel이 몇개 있는지 뽑아낸다.
2. HOG/SIFT features : edge의 방향 이 feature가 된다. 9가지의 edge 방향을 정해놓고 이미지에서 각 edge가 몇개씩 있는지 뽑아낸다.
3. Bag of Words : 이미지의 여러지점들 (local patch) 을 벡터로 모아서 큰 사전처럼 모아놓고, linear classifier를 적용한다.
공통점은
1. 먼저 feature를 추출하고 모은다(concatenation)
2. 모든 feature를 linear classifier에 넣는다.
그에 반해 딥러닝, CNN에서는
" feature를 추출하지 않고, 이미지자체를 classifier에 던져주고, 결괏값에 따라서 초기의 classifier를 훈련"시킨다.
그렇기 때문에, 기존의 W를 수정해나가는 과정이 필요하고 이를 Back propagation (역전파) 라고 하고
이에 대해서는 다음강의에서 배워본다 ~~
숨막히는 어려움... ^^
다른강의에서 몇번 다뤘던 내용이지만, softmax함수를 그냥 여기서 쓴다! 이렇게 하고 넘어갔지, 함수가 어떻게 생겼고 그래서 왜 쓰는지 그런건 생각하지 않았던 내용이라서 새로웠다... 하지만 역시 기초를 튼튼히 쌓아야 나중에 쉽게 무너지지 않을거라고 생각한당 👏😃
출처
'코딩 독학 > CS231n' 카테고리의 다른 글
| [cs231n] 4강. Backpropagation and Neural network (0) | 2020.10.31 |
|---|---|
| [cs231n] 과제1. KNN classifiers (0) | 2020.10.29 |
| [CS231n] 2강. L1 & L2 distance (0) | 2020.10.18 |
| [CS231n] 2강. Image classification (0) | 2020.10.16 |
| [CS231n] 1강. Introduction to Convolutional Neural Networks for Visual Recognition (0) | 2020.10.09 |





댓글