C1W2L10. Gradient Descent on m Examples
앞에서는 단일샘플에 대하여 경사하강법을 구현했다면, 이번에는 m개의 샘플에 대해 구현해보자.

m개의 (x, y) 샘플이 있고 x는 피처값, y는 참/거짓을 나타내는 레이블값이다. 샘플간의 구분을 위해 i번째 샘플임을 위첨자로 나타냈다.
m개의 샘플 전체에 대해 가중치 (w,b)를 적용한 비용함수 J(w,b)는 각샘플의 손실함수 L(a, y) 의 평균을 낸 것과 같다.
마찬가지로 도함수도 각 샘플의 도함수를 평균낸 것과 같다.
이것을 통해 경사하강법에 사용할 전체적인 경사를 구할 수 있다.
이것을 코드로 구현해보면 다음과 같다.


1. 먼저 값을 초기화한다.
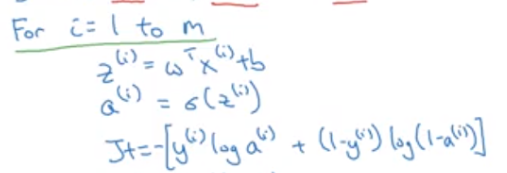
2. m개의 샘플에 대하여 z, a, J 식을 for문으로 작성한다.

3. 최종 w1, w2, b에 대한 도함수 dw1, dw2, db를 갱신하는 for문을 써준다!
요기서는 하나의 (x, y) 데이터에서 x 안에 특성이 2개 있다고 가정해서 가중치도 w1,
w2 로 두개뿐이라 for문을 안 썼는데, 특성이 여러개라면 for 문으로 식이 늘어날 것.
그렇게 m개의 샘플의 도함수값들을 다 더해서 m으로 나눠주면 끝!

4. 그리고 이렇게 가중치값들을 갱신하게 되고 한번의 경사하강법이 끝난다.
하지만 for loop을 사용한 경우 특성이나 샘플수가 늘어나면 시간이 오래걸린다는 단점이 있다. 이를 보정하기 위해 나온 것이 벡터화이다. 벡터화는 코드에서 for문을 없애는 마법이라고 불린다고 한다 🤣
C2W2L11. Vectorization

w와 x는 (1, n_x) 차원을 가진 벡터이다. 이들을 가지고 z = wTx + b 를 벡터화하지 않고 코드로 구현하면 왼쪽식처럼 복잡하게 풀어써야 한다.
하지만 파이썬의 np.dot(w,x) 식을 이용하면 한방에 z가 계산된다.
행렬곱을 위해 식 앞쪽의 w는 (n_x, 1)차원으로 변형시켜 행렬곱으로 빵 때려주는 것이다.
드디어 이 강좌에서 쥬피터 노트북을 켰당 😜

np.random.rand(1000000) 함수를 사용해 [0, 1) 범위의 무작위 값을 추출하여 균일한 분포를 갖는 x개의 난수를 갖는 배열(array)을 생성한다.
time.time() 으로 현재시각을 측정 (초단위)
np.dot(a, b) 로 벡터화한 행렬곱을 구한 뒤 time.time()을 구해
시간차를 구하면 내 컴퓨터에서는 105ms 가 걸린다.
근데 a와 b 배열의 1000000개의 원소들을 각각 곱해 c라는 배열을 반환하는 for문으로 계산해보면 1552ms나 걸림
(내 컴이 앤드류응교수님보다 10배 느림..)
아 그래서 벡터화를 하는구나 ~ 확실히 딥러닝 프로그램을 돌리면 30분씩도 걸리는데 이런게 큰 영향을 미칠 것이 확실함. ;;
C2W2L12. More Vectorization Examples
넘파이함수에는 벡터화 연산을 한방에 해주는 함수들이 많당!!
이걸 위에서 한 for문 경사하강법에 적용해보자

각 x(i) 는 n_x개의 특성을 갖는 배열이기 때문에
m개의 (x(i), y(i)) 샘플에 대해 각각 n_x개의 dw를 구해 갱신하는 두번째 for문이 필요하다.
두번째 for문을 벡터화해서 한줄로 바꿔버리자!
dw를 n_x개의 dw1, dw2, ... dw n_x 를 담는 배열로 바꾸기위해, np.zeros() 로 (n_x, 1) 차원의 배열로 초기화를 한 후 dw += x(i)dz(i) 로 갱신해준다
아직 잘 감이 살짝 안 온다. 배열도 헷갈리고 !! 다음 강에서 조금더 자세히 살펴보자..
'코딩 독학 > 앤드류응 딥러닝 Course1 (미래연구소 14기)' 카테고리의 다른 글
| C1W3L6~L7 (0) | 2020.10.13 |
|---|---|
| C1W2L1 ~ C1W2L4 (0) | 2020.10.09 |
| C1 W2 L13 ~ L14 (0) | 2020.10.09 |
| C1W2L4 ~ C1W2L9 (0) | 2020.10.07 |




댓글